Glossary mechanics of materials

Stress

Stress is defined as force per unit area. This is one of the most basic engineering quantities.

Shear stress has the same units as normal stress (force / area) but represents a stress that acts parallel to the surface (cross section). This is different from normal stress which acts perpendicular (normal) to the cross section. Torsion is a force that causes shear stress but this is not the only force that can cause shear stress. For example, a beam that supports a shear force also has a shear stress over the section (even without torsion).

Strain

Strain is the change in length per unit length. It is normally computed as (L_f - L₀) / L₀ where L_f is the final length and L₀ is the initial length. When testing materials, a gage length is normally specified known; this represents L₀.

Strain Rate

When testing a material, it is normally important to know how quickly (or slowly) it is being deformed or loaded. One way to report this is the amount of strain that occurs in a unit of time which is termed the strain rate. Because strain is dimension-less, units for this quantity are 1/time but sometimes it will be seen with the non-dimensional part attached e.g., in/in/sec.

Young's Modulus

This is the constant of proportionality between stress and strain. Units of this quantity are the same as stress (i.e., force per unit area) and the most commonly used are psi, Pa (Pascal), and MPa (Mega-Pascal). This is one of the most fundamental material properties. A typical value for steel is 29 x 10⁶ psi (200 GPa).

Deflection Equation

A prismatic bar loaded uniaxially made from a material that obeys Hooke's law deflects when loaded by an amount d=PL/AE where

d = Deflection

P = Applied Force

L = Length

A = Area

E = Young's Modulus

Poisson's Ratio

This is the ratio of lateral strain to longitudinal strain. The typical range of values for this quantity is between zero and 0.5.

Hooke's Law

When the applied force is proportional to the deflection, a material is said to obey Hooke's law. There is a linear relationship between the force and displacement and thus, linear elastic materials obey this law. When steel is below the proportional limit it shows this linear behavior.

Material Properties

These are properties specific to the material used. These are different from section properties which do not depend on what an object is made of. Examples of material properties are Young's modulus and yield point. Typical values of these for steel are 29 x 10⁶ psi and 36 ksi respectively. In general, different materials will have different material properties.

Section Properties

These are properties specific to the geometry (dimensions) of the setion used. These are different from material properties which depend on what an object is made of. Examples of section properties are area, diameter, and section modulus.

Stress - Strain Diagram

The stress-strain diagram is a plot Elasto-plastic stress-strain graph

of the stress on the ordinate (y-axis) versus the strain on the abscissa (x-axis). The data is often obtained from a uniaxial tension test although this is not the only test possible. The axes must be labeled with the appropriate units for stress (strain is dimensionless).

Proportional Limit

The proportional limit is the greatest stress that one can still see a linear relation between stress and strain. Beyond this point, the stress is no longer proportional to the strain.

Nominal

A nominal dimension is one that gives the intended or approximate size but this may (and often does) vary from the actual dimension. For example, a common lumber shape is a 2x4 but this is a nominal size and the actual dimensions are 1.5" x 3.5". The word is from Latin, of a name, nomin-, nomen name thus can be thought of as 'what we call it'.

Von-Mises

Richard von Mises was born 19 April 1883 in Lemberg, Austria (now Lvov, Ukraine). The von Mises Criterion (1913), also known as the maximum distortion energy criterion, octahedral shear stress theory, or Maxwell-Huber-Hencky-von Mises theory, is often used to estimate the yield of ductile materials. The von Mises criterion states that failure occurs when the energy of distortion reaches the same energy for yield/failure in uniaxial tension. Mathematically, this is expressed as,

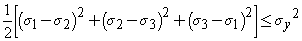
In the cases of plane stress, s₃ = 0. The Von Mises criterion reduces to,

Torsion And Warping

Thin-walled beams with open cross-section have very small torsional stiffness. It is therefore important for their proper use that transverse loads are applied without introducing too much torsion. This is determined by the distance between the line of load application and the shear center of the cross-section, and the determination of the shear center is therefore an essential ingredient of the analysis of thin-walled beams. If a thin-walled beam with open cross-section is loaded in torsion the twist of the beam is determined by two mechanisms: the classical St. Venant torsion stiffness determined by the shear modulus, and a contribution arising from constraining the warping of the cross-sections associated with St. Venant torsion. If the rate of twist is constant throughout a beam, the warping of all cross-sections is identical, and the second contribution vanishes. This mode of torsion is called homogeneous torsion, while the case of variable rate of twist is called non-homogeneous torsion. Non-homogeneous torsion introduces axial stresses in the beam that may have to be included in a strength analysis. The fact that thin-walled beams with open cross-section are very in torsion also in-their stability behavior. While columns with solid cross-section buckle in bending, thin-walled columns may buckle in a combined bending-torsion mode, associated with a lower buckling load. The details of the coupling depends on the shape of the cross-section and the application of the load

Precision

The precision of a measuring instrument is its least count (i.e., the smallest directly readable value). The precision of a data set is the closeness of agreement of results, often measured by standard deviation. When a value varies within statistical limits, the variations stem from numerous chance causes due to unknow factors, individually small, that are not readily identifiable or detectable. Within statistical limits, the average can be used as a good representation of the data set. Precision does not ensure accuracy.

Accuracy

Accuracy is the agreement between the test result and the "actual" value. For example, if the actual length of a rod is 230.0000 mm, a measurement of 231 mm is accurate to 0.4%. A different measurement of 232.15 mm is less accurate even though more precise. Accuracy does not ensure precision.

Linear Elastic Material

This is a material that responds both linearly and elastically when loaded and unloaded. Linear indicates that the stress is proportional to the strain and the material obeys Hooke's law. Elastic indicates that it follows the same path on the stress-strain diagram for both loading and unloading (i.e., no permanent deformation when load is released). Most materials have a linear elastic range which means that the above is valid for a certain load (stress) range but beyond this, the material may yield, become nonlinear, or both.

Modulus of Resilience

This is a material property and a measure of the energy a material can contain. It is the area under the stress-strain diagram up to the proportional limit.

Toughness

This is a material property and a measure of the energy a material can contain. It is the area under the entire stress-strain diagram (up to the point of failure).

Yield Point

This is a material property that indicates when permanent deformation will occur. If a material is loaded below its yield point, there will theoretically be no permanent deformation. This link will show a sample diagram in a new browser window with this and other terms.

Ultimate Stress

This is a material property that indicates the maximum stress the material has been observed to sustain.

Gage Length

This is the initial distance between two points that a measurement is being taken. As the test proceeds, this distance will change but the original distance will always be the same and this is what is used when computing strain.

Euler Buckling Load

When a column is loaded axially in compression, it is possible for it to become unstable before the material reaches its yield point. This load is termed the 'buckling load' or often the 'Euler buckling load' and is described by P_cr = pi² * E I / L².

Neutral Axis

A beam in flexure has tension on one side (e.g., the bottom face) and compression on the other (e.g., the top face). Somewhere between these two, there is a location of zero strain and this is the location of the neutral axis. If the section is symmetric (in both geometry and materials) the neutral axis is at the geometric centroid. TODO

Saint-Venant

Saint-Venant's Principle. It can be stated as follows: If a set of self-equilibrating loads are applied on a body over an area of characteristic dimension d, the internal stresses resulting from these loads are only significant over a portion of the body of approximate characteristic dimension d. Note that this principle is rather vague, as it deals with 'approximate' characteristic dimensions. It allows qualitative rather that quantitative conclusions to be drawn. An important application of Saint-Venant's principle deal with end effects in bars and beams.